Java - Heap Dump, Thread Dump and Core Dump

Dump 就是对程序运行时内存上的信息进行转储, 让我们可以查看程序当时的运行情况. Dump 对于调优和排错是非常有用的工具.

Heap Dump

Java 运行时对象分配在堆内存上, Heap dump 就是对堆内存进行转储.

生成

Heap dump 的生成有两种方式:

1) 运行 Java 程序时添加 -XX:+HeapDumpOnOutOfMemoryError 选项, 这样当程序发生 Out of Memory 错误时就会自动生成一份 Heap dump.

2) 使用 jmap 工具生成. 首先我们用 jps 找到程序的 pid (严谨点说其实是 lvmid), 然后运行:

jmap -dump:live,format=b,file=heap.bin <pid>

分析

可以使用 Java 自带的 jhat 工具来分析 Heap dump:

jhat <heap dump file>

等待一会, 就会提示

Started HTTP server on port 7000
Server is ready.

这时候浏览器中访问 127.0.0.1:7000 就可以了.

但是, jhat 在分析较大的 Heap dump 时效率比较差, 所以推荐使用 eclipse 提供的 Memory Analyzer (MAT) 来分析.

Thread Dump

Thread dump 转储的是线程相关的内存数据 (例如该线程的调用栈). Thread dump 有时候也被称为 javacore, 不过好像 javacore 是 IBM 虚拟机才有的.

生成

可以使用自带的 jstack 生成 Thread dump:

jstack <pid> >> thread.dump

分析

Thread dump 就是个文本文件格式, 直接打开查看就可以了.

Intellij IDEA 提供 Stacktrace 的分析, 我们可以用它来分析 Thread dump, 这样可以方便的知道某个线程运行到哪里.

打开 Intellij IDEAD -> Analyze -> Anaylyze Stacktrace..., 把 Thread dump 的内容复制粘贴进去, 确认即可.

Core Dump

上面提到的 Heap dump 和 Thread dump 都是和 Java 直接相关的, Core dump 则是操作系统提供的, 所有程序在意外退出时, 操作系统都可以生成 Core dump.

Core dump 包含了程序运行时的所有内存信息, 所以我们可以使用 Core dump 同时分析堆内存和运行时栈.

生成

默认操作系统是不生成 Core dump 的, 我们需要先打开:

# 如果你用的是 bash
ulimit -c unlimited

# 如果你像我一样用的是 zsh
limit coredumpsize unlimited

ulimit/limit 是设置 dump 的大小的, 默认为 0 也就是不 dump. 我们可以使用下面的命令来查看当前设置的大小:

# 如果你用的是 bash
ulimit -c

# 如果你像我一样用的是 zsh
limit coredumpsize

确认打开后, 我们可以使用 kill -ABRT <pid> 来生成 Core dump. 不过需要注意的是, 使用这种方法只有在当前 Terminal 下运行的 Java 程序才能生成 Core dump. 也就是说, 你必须在打开了 Core dump 的 Terminal 下运行 Java 程序, 这样 kill -ABRT <pid> 才会生成 Core dump. 如果你 Java 程序运行在一个没有打开 Core dump 的 Terminal 下, 那么即使你的 kill -ABRT <pid> 运行在打开了 Core dump 的 Terminal 下, 这时候 Core dump 也是不会生成的.

我们也可以使用 gcore 来生成生成 Core dump. 使用这个方法就无所谓你有没有使用 ulimit/limit 打开 Core dump 了.

sudo gcore <pid>

Mac 下 Core dump 生成在 /cores/ 文件夹下.

分析

我们可以使用 gdb 来分析 Core dump 文件.

Java 自带的 jstack 和 jmap 也可以用来分析 Core dump:

jstack <executable> <core dump file>
jmap <executable> <core dump file>

这里的 <executable> 指的是你运行 Java 程序时使用的 java, 一般可以用 $JAVA_HOME/bin/java 代替. 如果你指定的 java 和你运行用的 java 不是同一个版本, 就会抛出 sun.jvm.hotspot.debugger.UnmappedAddressException.

另外你使用的 jstack 和 jamp 也需要是相应的版本, 否则会提示 Can't attach to the core file.

Mac 编译 OpenJDK 7

因为 OpenJDK 7 发布已经很多年了, 所以想要在现在系统环境下编译成功还是有很多坑需要填的.

环境准备

1. OpenJDK 7 源码

   编译首先需要的肯定是源码啦, 1) 可以使用 Mercurial 从 http://hg.openjdk.java.net/jdk7u/jdk7u/ clone

   2) 也可以从 http://jdk.java.net/java-se-ri/7 下载压缩包. 这种方法通常获取到的并不是最新版本, 我下载到的是 7u75 的版本.

2. Xcode

   直接从 AppStore 上下载安装. 安装成功后运行下面的命令来安装 Command Line Tools:

    xcode-select --install
   

   Xcode 从 5 开始不再自带 gcc/g++ 了, 我们手动链接下:

    sudo ln -s /usr/bin/llvm-gcc /Applications/Xcode.app/Contents/Developer/usr/bin/llvm-gcc
    sudo ln -s /usr/bin/llvm-g++ /Applications/Xcode.app/Contents/Developer/usr/bin/llvm-g++
   

3. Ant <= 1.9.x

   Ant 从 1.10 开始不再支持 Java 8 之前的版本, 我们这里是编译 OpenJDK 7, 所以只能使用 1.9.x 或之前的版本.

4. CUPS

   去官网下载解压缩即可.

5. XQuartz

   编译需要 FreeType, 直接下载 XQuartz 安装即可.

6. BootJDK

   编译需要 JDK 环境 (鸡生蛋, 蛋生鸡的既视感, 编译第一个版本的 JDK 肯定是不需要 BootJDK 的), 去 Java SE 7 Archive Downloads 下载安装即可, 需要注意的是不要选版本号大于你源码的版本号的版本, 我选择的是 7u10 的.

7. 环境变量

    # 让 make 找到 Ant
    export ANT_HOME=<Ant 解压缩后的文件夹>
    # CUPS
    export ALT_CUPS_HEADERS_PATH=<CUPS 解压缩后的文件夹>
    # 设置 BootJDK
    export ALT_BOOTDIR=`/usr/libexec/java_home -v 1.7`
    # 生成 debug 版本
    export SKIP_DEBUG_BUILD=false
    # 取消 JAVA_HOME 和 CLASSPATH 变量
    unset JAVA_HOME
    unset CLASSPATH
   

完成以上步骤之后, 运行 make sanity 应该就能看到 Sanity check passed. 字样了, 不过如果你这时候运行 make 编译肯定会报错的, 下面请继续阅读 “填坑指南”.

填坑指南

1. error: equality comparison with extraneous
   error: '&&' within '||'
   

   这是因为编译器语法校验太严格了, 添加环境变量 export COMPILER_WARNINGS_FATAL=false 即可.

2. clang: error: unknown argument: '-fpch-deps'
   

   这是因为新的编译器已经不再支持这个选项了, 打开 hotspot/make/bsd/makefiles/gcc.make, 找到 DEPFLAGS = -fpch-deps -MMD -MP -MF $(DEP_DIR)/$(@:%=%.d) 这一行, 删掉其中的 -fpch-deps 即可.

3. error: friend declaration specifying a default argument must be a definition
    inline friend relocInfo prefix_relocInfo(int datalen = 0);
   error: friend declaration specifying a default argument must be the only declaration
    inline relocInfo prefix_relocInfo(int datalen) {
   error: 'RAW_BITS' is a protected member of 'relocInfo'
    return relocInfo(relocInfo::data_prefix_tag, relocInfo::RAW_BITS, relocInfo::datalen_tag | datalen);
   error: calling a protected constructor of class 'relocInfo'
    return relocInfo(relocInfo::data_prefix_tag, relocInfo::RAW_BITS, relocInfo::datalen_tag | datalen);
   

   这个错误报的不是很明显, 因为 error 隐藏在一堆 warning 中, 需要往上翻页很久才能看到, 所以如果看到 make 输出 488 warnings and 4 errors generated. 那么基本上就是这个错误了.

   这个错误也是编译器版本太新导致的, 原先的 C++ 的一些语法已经不再支持了.

   打开 hotspot/src/share/vm/code/relocInfo.hpp

   找到 inline friend relocInfo prefix_relocInfo(int datalen = 0); 这一行, 改成 inline friend relocInfo prefix_relocInfo(int datalen);.

   找到 inline relocInfo prefix_relocInfo(int datalen) { 这一行, 改成 inline relocInfo prefix_relocInfo(int datalen = 0) {.

   最后保存即可.

4. java.lang.NullPointerException
    at java.util.Hashtable.put(Hashtable.java:542)
    at java.lang.System.initProperties(Native Method)
    at java.lang.System.initializeSystemClass(System.java:1115)
   

   设置环境变量 export LANG=C 即可

5. Error: time is more than 10 years from present: 1136059200000
   java.lang.RuntimeException: time is more than 10 years from present: 1136059200000
    at build.tools.generatecurrencydata.GenerateCurrencyData.makeSpecialCaseEntry(GenerateCurrencyData.java:285)
    at build.tools.generatecurrencydata.GenerateCurrencyData.buildMainAndSpecialCaseTables(GenerateCurrencyData.java:225)
    at build.tools.generatecurrencydata.GenerateCurrencyData.main(GenerateCurrencyData.java:154)
   

   如果你是使用 Mercurial clone 的最新代码就不会遇到这个问题, 我下载的 7u75 存在这个问题.

   打开 jdk/src/share/classes/java/util/CurrencyData.properties, 搜索 200, 把所有的年份改成距今不超过 10 年的年份即可.

6. error: JavaNativeFoundation/JavaNativeFoundation.h: No such file or directory
   

   这个问题应该是 BootJDK 有问题导致的, 我系统原先就装有 7u65, 把该版本作为 BootJDK 编译后报这个错误, 重新下载了 7u10 安装, 然后修改 ALT_BOOTDIR 到对应的版本就解决了.

7. Undefined symbols for architecture x86_64:
   "_attachCurrentThread", referenced from:
    +[ThreadUtilities getJNIEnv] in ThreadUtilities.o
    +[ThreadUtilities getJNIEnvUncached] in ThreadUtilities.o
   ld: symbol(s) not found for architecture x86_64
   clang: error: linker command failed with exit code 1 (use -v to see invocation)
   

   当定义了环境变量 SKIP_DEBUG_BUILD=false 时会报这个错误.

   打开 /jdk/src/macosx/native/sun/osxapp/ThreadUtilities.m, 将:

   inline void attachCurrentThread(void** env) { 修成成:

   static inline void attachCurrentThread(void** env) {

填完上面的这些坑, 应该就能编译成功了. 编译好之后运行 ./build/macosx-x86_64/bin/java -version 如果输出类似下面的信息就说明编译成功了:

openjdk version "1.7.0-internal"
OpenJDK Runtime Environment (build 1.7.0-internal-yoncise_2017_05_21_16_54-b00)
OpenJDK 64-Bit Server VM (build 24.75-b04, mixed mode)

仅编译 HotSpot

大部分情况下我们关心的是 jvm 的运行情况, 所以只需要编译 HotSpot, 这样可以节省下很多编译时间.

首先切换到 hotspot/make 目录下. 按照之前说的把环境变量设置好.

修改 ./bsd/makefiles/buildtree.make 中的 env.sh rule. 将:

env.sh: $(BUILDTREE_MAKE)
	@echo Creating $@ ...
	$(QUIETLY) ( \
	$(BUILDTREE_COMMENT); \
	[ -n "$$JAVA_HOME" ] && { echo ": \$${JAVA_HOME:=$${JAVA_HOME}}"; }; \
	{ \
	echo "CLASSPATH=$${CLASSPATH:+$$CLASSPATH:}.:\$${JAVA_HOME}/jre/lib/rt.jar:\$${JAVA_HOME}/jre/lib/i18n.jar"; \
	} | sed s:$${JAVA_HOME:--------}:\$${JAVA_HOME}:g; \
	echo "HOTSPOT_BUILD_USER=\"$${LOGNAME:-$$USER} in `basename $(GAMMADIR)`\""; \
	echo "export JAVA_HOME CLASSPATH HOTSPOT_BUILD_USER"; \
	) > $@

修改成:

env.sh: $(BUILDTREE_MAKE)
	@echo Creating $@ ...
	$(QUIETLY) ( \
	$(BUILDTREE_COMMENT); \
	[ -n "$$JAVA_HOME" ] && { echo "JAVA_HOME=$${JAVA_HOME}"; }; \
	{ \
	echo "CLASSPATH=$${CLASSPATH:+$$CLASSPATH:}.:\$${JAVA_HOME}/jre/lib/rt.jar:\$${JAVA_HOME}/jre/lib/i18n.jar"; \
	} | sed s:$${JAVA_HOME:--------}:\$${JAVA_HOME}:g; \
	echo "HOTSPOT_BUILD_USER=\"$${LOGNAME:-$$USER} in `basename $(GAMMADIR)`\""; \
	echo "LD_LIBRARY_PATH=."; \
	echo "LANG=C"; \
	echo "export JAVA_HOME CLASSPATH HOTSPOT_BUILD_USER LD_LIBRARY_PATH LANG"; \
	) > $@

然后运行 make 编译. 建议第一次编译把输出重定向到 /dev/null, 编译会加快不少.

编译成功后, 切换到 hotspot/build/bsd/bsd_amd64_compiler2/product 目录, 运行:

# 设置环境变量
. ./env.sh
# 运行 test_gamma 需要设置环境变量 LANG=C, 不然会报 NPE
./test_gamma

正常输出不报错就说明编译好了. 该目录下的 ./gamma 就是 HotSpot 的启动程序.

版本号

JDK 从 1.5 开始, 官方就不再使用类似 JDK 1.5 的名称了, 只有在开发版本号 (Developer Version, java -version 的输出) 中继续沿用 1.5, 1.6 和 1.7 的命名方式, 公开版本号 (Product Version) 则使用 JDK 5, JDK 6 和 JDK 7 的命名方式.

有时候下载 JDK 看到 7u75, 8u45 的版本号, 这里的 u 表示的是 update.

Re: JDK7 build on mac os fails: JavaNativeFoundation.h: No such file

Compilation failure related to Time [Error: time is more than 10,years from present: 1136059200000]

第一章 Mac os下编译openJDK 7

Mac编译OpenJDK 7

Mac下编译openJDK

libosxapp.dylib fails to build on Mac OS 10.9 with clang

Backward 总结

完成 cs231n assignment 2 中 bachnorm_backward 函数花费了不少时间, 稍微总结下.

计算 Backward 主要分为两种方法 1). On paper 2). Computation graph

本质是一样的, 都是利用 Chain rule. 但我个人更偏爱 Computation graph, 对于复杂的函数会更清晰, 尤其是当我们在处理矩阵时.

下面我们以计算方差 var = np.var(x, axis=0) 为例来说明两种方法 (x.shape 为 (n, d)).

On paper

首先我们要明确一点, 因为 var 和 x 都是多维的, 所以我们最终要求的并不是 \(\frac{dvar}{dx}\), 而是 \(\frac{dout}{dx}\), out 是在 var 基础上得到的一个标量, 假设 out = np.sum(var).

我们有:

根据 Chain rule:

下面我们推导最关键的 \(\frac{dvar_{j}}{dx_{ij}}\):

最后就是看怎么推广到矩阵. 这个步骤极容易出错, 这也是为什么我偏爱用 Computation graph 的原因!

Computation graph

首先我们把计算过程变成图, 图的节点为操作数或操作符. 尽量把计算过程分解成比较简单的运算.

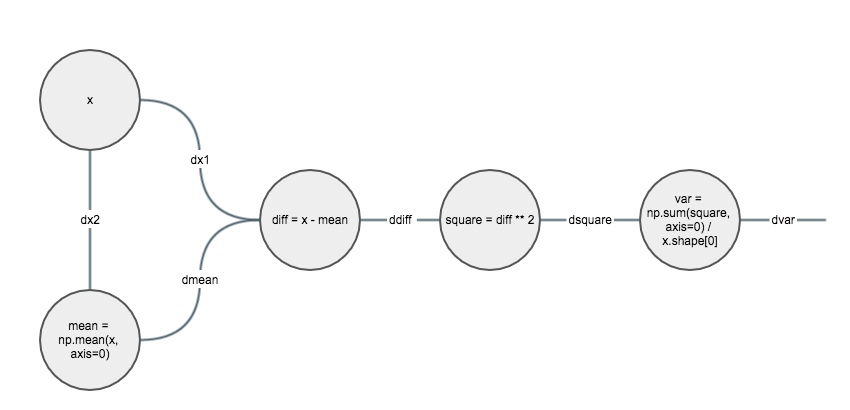
然后就是按照从后往前的顺序一步步计算. 因为都是简单操作, 所以我们可以尝试根据 shape 来思考.

比如 x, w, dout 的 shape 分别为 (N, D), (D, M) 和 (N, M), 因为 dx 的 shape 应该和 x 一样为 (N, D), 所以我们就可以得出 dx = dout.dot(w.T). (假设这里 out = x.dot(w))

下面我们就一个个来计算:

dsquare = dvar / x.sahpe[0]
ddiff = 2 * (x - mean) * dsquare
dmean = -np.sum(ddiff, axis=0)
dx1 = ddiff
dx2 = dmean / x.shape[0]
dx = dx1 + dx2

其实 Computation graph 就是在每个节点上应用 On paper, 只是每个节点都是简单操作, 所以不容易出错也好理解.

Backpropagation, Intuitions

numpy Broadcasting 和 Advanced Indexing

Broadcasting

Broadcasting allows universal functions to deal in a meaningful way with inputs that do not have exactly the same shape.

Universal functions 简单理解就是 elementwise 的函数.

Broadcasting 就两条规则:

1. 如果两个数组的 ndim 不一样, 那么就向 ndim 小的数组的 shape prepend 1, 直到两个数组的 ndim 一样.

   比如: 数组 a 和 b 的 shape 分别为 (3, 4) 和 (4), 那么, 根据规则, 会将 b 的 shape 变成 (1, 4) (注意是 prepend, 所以不是变成 (4, 1))

2. 如果两个数组在某个维度的 size 不一致且其中一个数组的 size 为 1, 那么就将 size 为 1 的数组沿着这个维度复制, 直到 size 和另一个数组一致.

   比如: 数组 a 和 b 的 shape 分别为 (3, 4) 和 (1, 4)

    >>> b
    array([[0, 1, 2, 3]])
   

   那么 numpy 会将 b 当做:

    array([[ 0.,  1.,  2.,  3.],
           [ 0.,  1.,  2.,  3.],
           [ 0.,  1.,  2.,  3.]])
   

Advanced Indexing

所谓 Advanced Indexing 就是, a[obj] 中的 obj 属于下面三种情况:

1. 不是 tuple 的 sequence
2. 是 ndarray (值为 Integer 或 Boolean)
3. 是一个 tuple 但其中的值除了包括 int 和 slicing, 至少有一个是 sequence 或 ndarray (值为 Integer 或 Boolean)

Advanced Indexing 分为两种情况: 1). Integer 的数组 2). Boolean 的数组.

Integer

数组 a 接受 a[idx0, idx1, idx2, ...] 形式的 indexing, 其中 idx0, idx1… 的 shape 要一致 (或者可以经过 Broadcasting 后一致) 且 idx 的数量要小于等于 a.ndim.

假如 idx0 = np.array([2, 1]), idx1 = np.array([2]).

那么 a[idx0, idx1] 的结果为:

1. 将 idx0 和 idx1 “合并” (经过 Broadcasting 后两个数组的 shape 将会”一致”, 将相应位置的元素合并):

    [(2, 2), (1, 2)]
   

2. 最终结果为:

    [a[2, 2], a[1, 2]]
   

Integer 数组和 slicing 结合

当 index 里出现 slicing (start:end:step) 对象和 Integer 数组混合使用的情况时, 结果会变得比较复杂.

我们可以从最终结果的 shape 来理解这一情况. 当 slicing 和 Integer 数组混合使用时, 有两种情况:

1. slicing 位于Integer 数组之间. 比如: a[[0, 2], :, 1] (这里的 1 相当于 [1], 因为现在讨论的是 Advanced Indexing)

2. Integer 数组之间没有 slicing. 比如: a[..., [0, 1], [1, 2], :]

在第一种情况下, 我们假设多个 Integer 数组经过 Broadcasting 后的 shape 为 shapeA, slicing 组成的 shape 为 shapeB, 那么最终的 shape 为 (shapeA, shapeB), Integer 数组最终的 shape 被提到了最前面. 比如:

>>> a = np.arange(24).reshape(3, 2, 4)
>>> a[[0, 1, 2], :, 1].shape
(3, 2)

第二种情况, Integer 数组最终的 shape 会在原来的位置. 比如:

>>> a = np.arange(81).reshape(3, 3, 3, 3)
>>> a[:, [[0, 1], [0, 1]], [0, 2] , :].shape
(3, 2, 2, 3)

下面看一个比较复杂的例子:

>>> a = np.arange(243).reshape(3, 3, 3, 3, 3)
>>> a[:, [[0, 1], [0, 1]], [0, 2] , :, [0, 1]].shape
(2, 2, 3, 3)

知道了 shape 之后, indexing 的结果就比较好得出了, 根据 shape, 看对应的是哪个维度在变化就好了.

Boolean

Boolean 数组的 indexing 分为两种情况:

1. 数组 a 接受 a[idx] 形式的 indexing, 其中 idx.ndim = a.ndim (不是 shape).

   a[idx] 的结果为 ndim 为 1 的数组, 内容由 a 中 idx 在相同位置值为 True 的数据组成 (如果 a 中存在找不到对应 idx 中的值, 则视为 False. 如果 idx 中存在找不到对应 a 中的值, 则报错).

2. 数组 a 接受 a[idx0, idx1, ...] 形式的 indexing, 其中 idx0, idx1… 的 ndim 为 1. 那么 a[idx0, idx1, ...] 等价于 a[np.arange(idx0.size)[idx0], np.arange(idx1.size)[idx1], ...]

   也就是说使用多个 Boolean 数组 indexing 时, Boolean 数组会先转化成 np.arange(<Boolean 数组>.size)[<Boolean 数组>] 的 Integer 数组.

   比如:

    >>> a = np.arange(12).reshape(3, 4)
    >>> idx0 = np.array([True, False])
    >>> idx1 = np.array([False, True, True])
    >>> a[idx0, idx1]
    array([1, 2])
   

   那么 a[idx0, idx1] 等价于 a[np.array([0]), np.array([1, 2])] (这里会先 Broadcasting).

ps. indexing 时尽量使用 ndarray 而不是 python 自带的 list, 因为 a[[idx0, idx1, ...]] 等价于 a[idx0, idx1, ...] 而不等价于 a[np.array([idx0, idx1, ...]).

Broadcasting rules

Fancy indexing and index tricks

Advanced Indexing

链式法则推导

链式法则

链式法则 (chain rule), 是求复合函数导数的一个法则. 一元情况下, 设 \(f\) 和 \(g\) 为两个关于 \(x\) 可导函数, 则复合函数 \((f \circ g)(x) = f(g(x))\) 的导数 \((f \circ g)'(x)\) 为:

推导

一元的链式法则推导比较简单, 我们直接考虑二元的情况. 考虑函数 \(z = f(x, y)\), 其中 \(x = g(t), y = h(t)\), 那么:

因为 \(g'(t) = \lim_{\Delta t \to 0}\frac{g(t + \Delta t) - g(t)}{\Delta t}\), \(h'(t) = \lim_{\Delta t \to 0}\frac{h(t + \Delta t) - h(t)}{\Delta t}\), 所以:

根据导数的定义得:

令 \(s = t + \Delta t\), 得:

同样根据导数定义得:

同时, 当 \(\Delta t \to 0\) 时, \(s = t\):

注意点

1. 推导时把 \(t\) 当做常数. 虽然 \(s\) 会随着 \(\Delta t\) 的变化而变化, 但是当 \(\Delta t\) 确定时, \(s\) 是确定的
2. \(\Delta t\) 表示 实际 的增量, \(dt\) 表示 微小 的增量
3. \(f'(t)\) 是牛顿表示导数的符号, 莱布尼兹的表示方式是 \(\frac{dz}{dt}\)
4. \(\frac{\partial z}{\partial x}\) 表示偏导数, \(\partial\) 是 \(d\) 的圆体变体
5. 二元以上的推导也是类似的