Uniswap V3 流动性

27 Aug 2025

Uniswap V3 主要解决的是 V2 资金利用率不高的问题，协议上允许流动性提供者 LP 只在一定的价格区间提供流动性。看似不大的改变，却让合约的实现变得非常复杂，究其原因就是不同的价格区间会有不同的流动性。

一个价格区间

先看只有一个价格区间的情况。和 V2 类似，但只有在指定的价格区间内的 token 是由 LP 提供的。下图中 c 点是当前池子的价格，也就是说 \(Price_{token_x} = \frac{y_c}{x_c}\)，a 点和 c 点是 LP 指定的价格区间。

如果是 V2 的池子，那么此时池子里有 \(x_c = x_b + x_{real}\) 的 X 和 \(y_c = y_a + y_{real}\) 的 Y，图中的储备金曲线满足 \(x_c * y_c = k\)。但在 V3 的池子里，此时只有 \(x_{real}\) 的 X 和 \(y_{real}\) 的 Y。注意，此时并没有 \(x_{real} * y_{real} = k\)，成立的依然是 \(x_c * y_c = k\) 即 \((x_b + x_{real}) * (y_a + y_{real}) = k\)。

如果 c 不在 a，b 之间呢？此时 \(x_c * y_c = k\) 仍然成立，但如果 c 在 a 点的右边，则 \(y_{real} = 0\), \(x_{real} = x_a - x_b\)，如果 c 在 b 点的左边，则 \(x_{real} = 0\)，\(y_{real} = y_b - y_a\)。

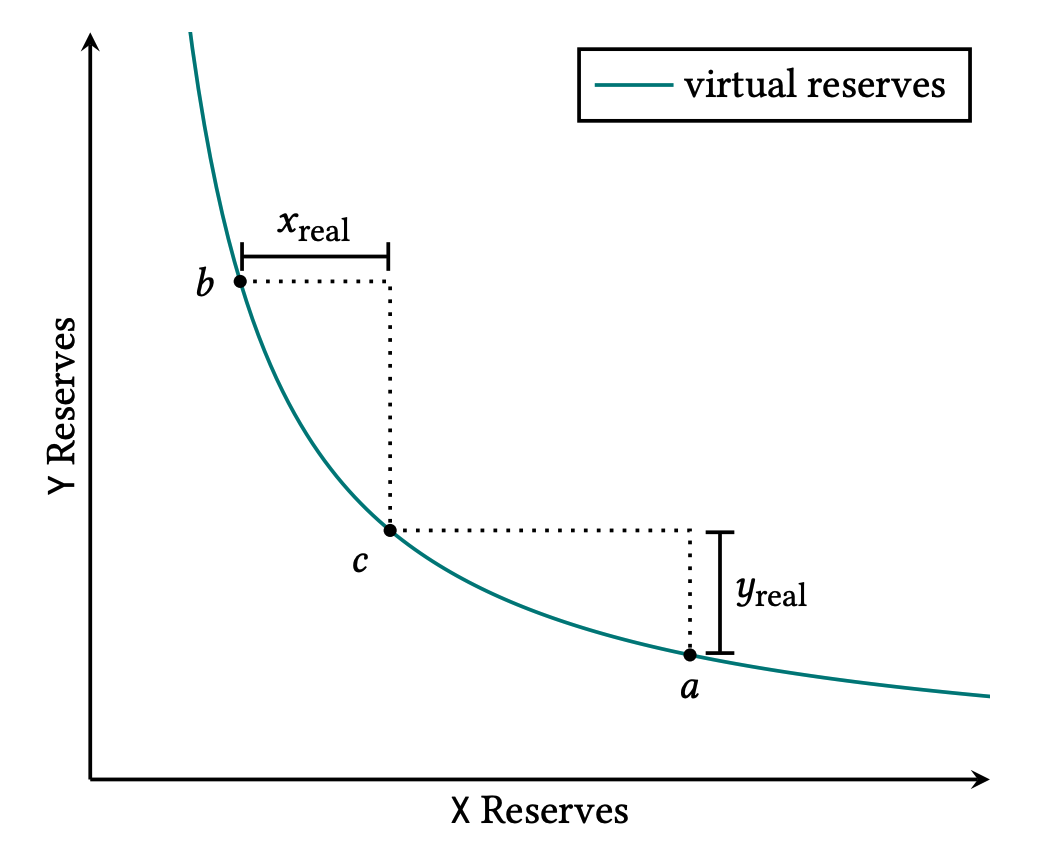
a 和 b 点的价格是已知，所以只要知道 k 就能算出 \(x_{real}\) 和 \(y_{real}\)，反之亦然。

多个价格区间

V3 下不同的 LP 可以在不同的价格区间提供流动性。此时我们总能将价格区间分成三种类型，一种是没有人提供流动性的，一种是只有一个 LP 提供流动性的，另一种是有多个 LP 提供流动性的。

没有人提供流动性的就不多说了。只有一个人提供流动性的就参考前面的一个价格区间里说的来处理。

对于多个 LP 提供流动性的我们要做的就是把他们进行合并。

第一个问题，为什么他们能进行合并？在 Uniswap V3 下，CFMM 计算时都是算上虚拟储备金的，所以合并多个 LP 的流动性可以理解为就是在 V2 下进行添加流动性。

第二个问题，是不是合并后满足 \((x_{lp1} + x_{lp2})(y_{lp1} + y_{lp2}) = k_{lp1} + k_{lp2}\) 呢？我们来看下，在 V2 下，不管当前池子的价格如何，每个 LP 中的 X 和 Y 的比例都是一样的。所以

\[ x_{lp1} = n * x_{lp2} \newline y_{lp1} = n * y_{lp2} \]

又因为

\[ x_{lp1} * y_{lp1} = k_{lp1} \newline x_{lp2} * y_{lp2} = k_{lp2} \]

所以

\[ x_{lp1} * y_{lp1} = n * x_{lp2} * n * x_{lp2} = n^2 * k_{lp2} \newline k_{lp1} = n^2 * k_{lp2} \]

两个池子合并后

\[ (x_{lp1} + x_{lp2})(y_{lp1} + y_{lp2}) = (n+1)^2 * x_{lp2} * y_{lp2} \newline (n+1)^2 * x_{lp2} * y_{lp2} = (n+1)^2 * k_{lp2} \]

显然

\[ k_{lp1} + k_{lp2} = (1 + n^2) * k_{lp2} \ne (n+1)^2 * k_{lp2} \]

但是我们发现

\[ \sqrt{k_{lp1}} + \sqrt{k_{lp2}} = (1 + n) \sqrt{k_{lp2}} = \sqrt{(n+1)^2 * k_{lp2}} \]

所以多个 LP 的 k 值的平方根的 和 等于合并后的 k 值的平方根。这也是为什么 Uniswap 要用 \(L = \sqrt{x * y}\) 来表示流动性，因为L之间有线性关系。