Backward 总结

30 Mar 2017

完成 cs231n assignment 2 中 bachnorm_backward 函数花费了不少时间, 稍微总结下.

计算 Backward 主要分为两种方法 1). On paper 2). Computation graph

本质是一样的, 都是利用 Chain rule. 但我个人更偏爱 Computation graph, 对于复杂的函数会更清晰, 尤其是当我们在处理矩阵时.

下面我们以计算方差 var = np.var(x, axis=0) 为例来说明两种方法 (x.shape 为 (n, d)).

On paper

首先我们要明确一点, 因为 var 和 x 都是多维的, 所以我们最终要求的并不是 \(\frac{dvar}{dx}\), 而是 \(\frac{dout}{dx}\), out 是在 var 基础上得到的一个标量, 假设 out = np.sum(var).

我们有:

\[\begin{align*} \frac{dout}{dx} &= \begin{bmatrix} \frac{dout}{dx_{00}} & .. & \frac{dout}{dx_{0d}} \\ .. & \frac{dout}{dx_{ij}} & .. \\ \frac{dout}{dx_{n0}} & .. & \frac{dout}{dx_{nd}} \end{bmatrix} \\ \frac{dout}{dvar} &= \begin{bmatrix} \frac{dout}{dvar_{0}} & .. & \frac{dout}{dvar_{d}} \end{bmatrix} \end{align*}\]

根据 Chain rule:

\[\begin{equation} \frac{dout}{dx_{ij}} = \sum_{k} \frac{dout}{dvar_{k}} \cdot \frac{dvar_{k}}{dx_{ij}} \end{equation}\]

下面我们推导最关键的 \(\frac{dvar_{j}}{dx_{ij}}\):

\[\begin{alignat*}{3} \frac{dvar_{j}}{dx_{ij}} &= \frac{d\frac{(x_{0j} - \bar{x})^2 + ... + (x_{ij} - \bar{x})^2 + ... + (x_{nj} - \bar{x})^2}{N}}{dx_{ij}} \\ &= \frac{2}{n} ((x_{ij} - \bar{x}) + \sum_{k} (x_{kj} - \bar{x})\frac{d\bar{x}}{dx_{ij}}) \\ \because & \sum_{k} (x_{kj} - \bar{x}) = 0 \\ \therefore & \frac{dvar_{j}}{dx_{ij}} = \frac{2(x_{ij} - \bar{x})}{n} \end{alignat*}\]

最后就是看怎么推广到矩阵. 这个步骤极容易出错, 这也是为什么我偏爱用 Computation graph 的原因!

Computation graph

首先我们把计算过程变成图, 图的节点为操作数或操作符. 尽量把计算过程分解成比较简单的运算.

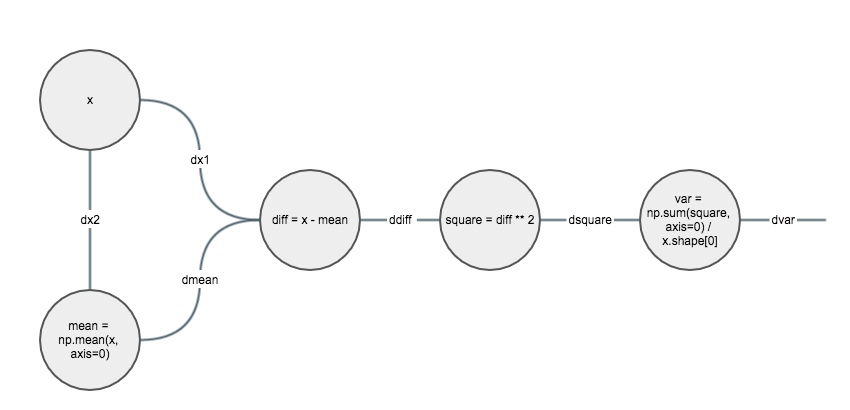
然后就是按照从后往前的顺序一步步计算. 因为都是简单操作, 所以我们可以尝试根据 shape 来思考.

比如 x, w, dout 的 shape 分别为 (N, D), (D, M) 和 (N, M), 因为 dx 的 shape 应该和 x 一样为 (N, D), 所以我们就可以得出 dx = dout.dot(w.T). (假设这里 out = x.dot(w))

下面我们就一个个来计算:

其实 Computation graph 就是在每个节点上应用 On paper, 只是每个节点都是简单操作, 所以不容易出错也好理解.

Backpropagation, Intuitions